Lab for L-functions and arithmetic

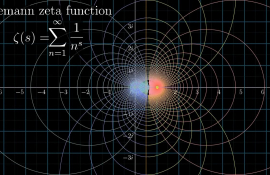
L-함수와 산술 연구실

관련기사 바로가기
L-함수와 산술 연구실

리만 이후로 L-함수는 산술연구의 가장 중요한 도구중의 하나이다. 다음은 우리 연구실의 몇 가지 연구주제들이다.
- 낮게 분토하는 L-함수의 영점들
- L-함수의 단순근들
- 극단적인 L-값들
-강한 아틴 추측의 수체의 응용들
- 타원곡선의 위수
Since Riemann, L-functions are one of the most importants tools to study arithmetic.
Below is some of the research topics in our Lab.
- Low-lying zeros of L-functions
- Simple zeros of L-functions
- Extremal L-values
- Applications of the strong Artin conjecture in number fields.
- Ranks of elliptic curves

Major research field

정수론, 아틴 엘-함수, 극대, 극소값 / Number Theory, Artin L-functions, extreme values

Desired field of research

임의 행렬, 엘-함수의 영점들 / Random matrix, zeros of L-functions

Research Keywords and Topics

정수론, 아틴 엘-함수, 극대, 극소값, 임의 행렬, 엘-함수의 영점들
Number Theory, Artin L-functions, extreme values, random matrix, zeros of L-functions

Research Publications
MORE

Int. Math. Res. Not. IMRN, The Average of the Smallest Prime in a Conjugacy Class, P.J. Cho and H.H. Kim, 202003

Compos. Math. Simple zeros of automorphic L-functions, A. R. Booker, P. J. Cho, and M. Kim, 2019

Int. Math. Res. Not. IMRN, n-level densities of Artin L-functions, P. J. Cho and H. H. Kim, 2015

국가과학기술표준분류

  • NA. 수학
  • NA01. 대수학
  • NA0103. 수론

국가기술지도분류

  • 기타 분야
  • 060000. 국가기술지도(NTRM) 99개 핵심기술 분류에 속하지 않는 기타 연구

녹색기술분류

  • 녹색기술관련 과제 아님
  • 녹색기술관련 과제 아님
  • 999. 녹색기술 관련과제 아님

6T분류

  • 기타 분야
  • 기타 분야
  • 070000. 위의 미래유망신기술(6T) 103개 세분류에 속하지 않는 기타 연구